已知
抛物线$\Gamma$方程为$y^2=4x$,焦点为$F$。直线$l$过焦点交$\Gamma$于A、B两点。C是抛物线上动点,$AC$、$BC$分别交抛物线的准线于D、E。
求证: $$ \overrightarrow{OE} \cdot \overrightarrow{OD} = -3 $$ 为定值。
题解
我也不知道这个题应该取个什么标题。索性叫X吧,因为图里会有交叉直线。
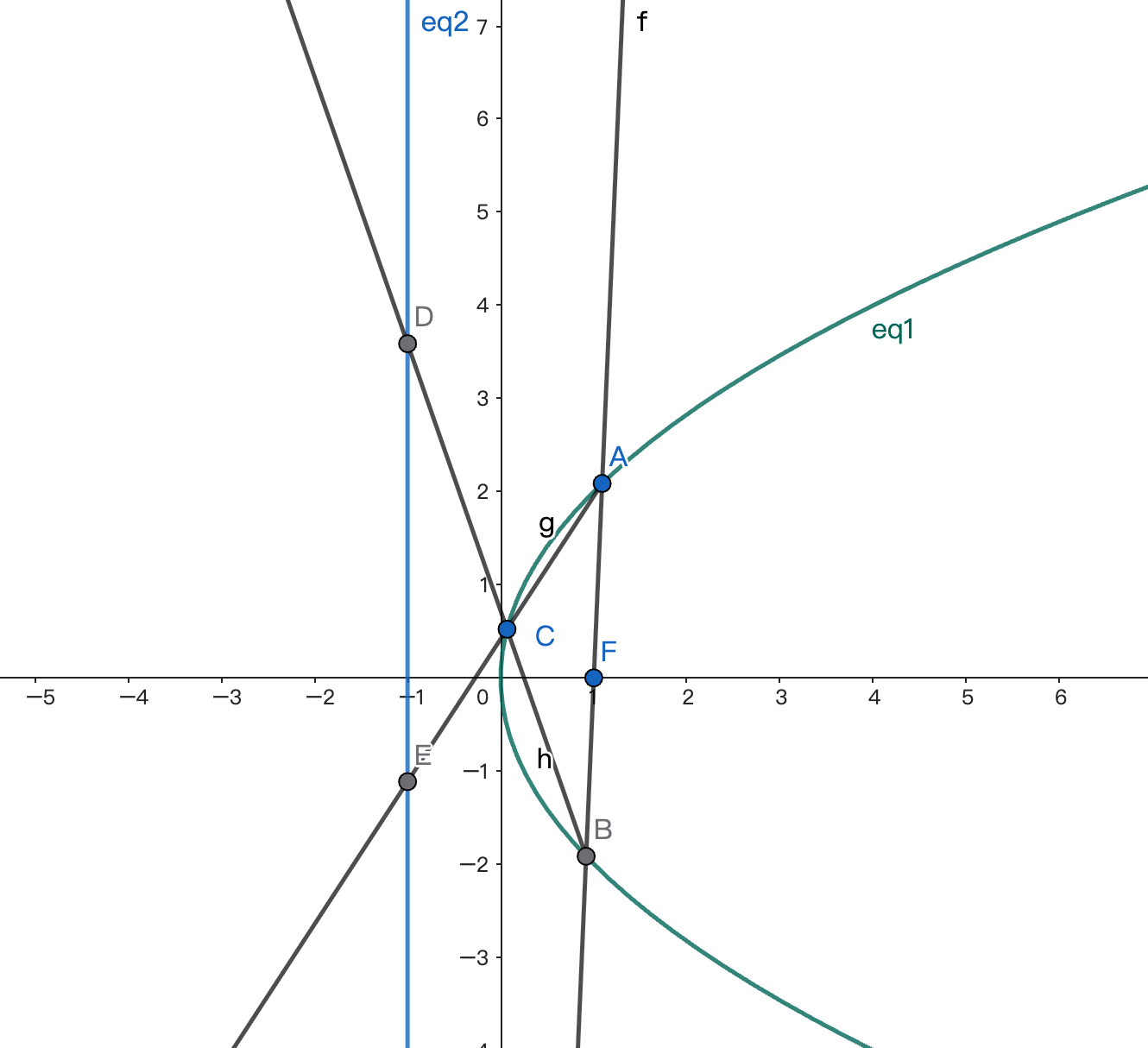
要证: $$ \overrightarrow{OE} \cdot \overrightarrow{OD} = -3 $$ 只要证: $$ y_D \cdot y_E = -4 $$
设线(单斜率)
最简单直接的想法就是:
设$l: x=ty+1$,和抛物线联立得到:
$$ y^2-4ty-4=0 $$
设$A(x_1,y_2)$以及$B(x_2,y_2)$,再设$\color{red}C(x_0, y_0)$。
那么: $$ y_1+y_2 = 4t, \quad y_1y_2 = -4 $$
直线$AC$的方程为: $$ \frac{y-y_0}{x-x_0} = \frac{y_1-y_0}{x_1-x_0} $$ 令$x=-1$得到$D$点的纵坐标: $$ y_D = y_0 + (-1-x_0)\frac{y_1-y_0}{x_1-x_0} $$ 其中 $$ \color{red} x_1-x_0 = \frac{1}{4}(y_1^2-y_0^2) = \frac{1}{4}(y_1-y_0)(y_1+y_0) $$ 所以: $$ \begin{aligned} &y_D \\ = &y_0 + (-1-x_0)\frac{4}{y_1+y_0}\\ = &\frac{y_0y_1+y_0^2-4-4x_0}{y_1+y_0}\\ = &\frac{y_0y_1-4}{y_1+y_0} \end{aligned} $$ 同理: $$ y_E = \frac{y_0y_2-4}{y_2+y_0} $$
那么: $$ \begin{aligned} &y_Dy_E \\ = &\frac{y_0y_1-4}{y_1+y_0} \cdot \frac{y_0y_2-4}{y_2+y_0}\\ = &\frac{y_0^2y_1y_2+16-4y_0(y_1+y_2)}{y_1y_2+y_0^2+y_0(y_1+y_2)}\\ = &\frac{-4y_0^2+16+16ty_0}{-4+y_0^2-4ty_0} = -4 \end{aligned} $$
设线陷阱
当然,上面设线法求解的过程中,我们用了很多技巧进行化简(也就是红色的部分)。
如果不使用他们,计算就会非常复杂,难以继续。
A、B的设法不变,我们设$\color{darkgreen}C(\frac{1}{4}m^2, m)$。
依然是: $$ y_D = m + (-1-\frac{1}{4}m^2)\frac{y_1-m}{x_1-\frac{1}{4}m^2} $$ 和 $$ y_E = m + (-1-\frac{1}{4}m^2)\frac{y_2-m}{x_2-\frac{1}{4}m^2} $$
这次我们直接相乘: $$ \begin{aligned} &y_D\cdot y_E \\ = &m^2 + (1+\frac{1}{4}m^2)^2{\color{green}\frac{y_1-m}{x_1-\frac{1}{4}m^2}\cdot\frac{y_2-m}{x_2-\frac{1}{4}m^2}}\\ &-m(1+\frac{1}{4}m^2)({\color{green}\frac{y_1-m}{x_1-\frac{1}{4}m^2}+\frac{y_2-m}{x_2-\frac{1}{4}m^2}}) \end{aligned} $$
其中: $$ \begin{aligned} &\frac{y_1-m}{x_1-\frac{1}{4}m^2}\cdot\frac{y_2-m}{x_2-\frac{1}{4}m^2}\\ = &\frac{y_1y_2-m(y_1+y_2)+m^2}{x_1x_2 - \frac{1}{4}m^2(x_1+x_2)+\frac{1}{16}m^4} \end{aligned} $$
我们已经计算过: $$ y_1+y_2 = 4t,\quad y_1y_2=-4 $$ 那么: $$ x_1+x_2 = \frac{1}{4}(y_1^2+y_2^2)=4t^2+2, \quad x_1x_2 = \frac{1}{16}y_1^2y_2^2 = 1 $$
所以: $$ \begin{aligned} &\frac{y_1-m}{x_1-\frac{1}{4}m^2}\cdot\frac{y_2-m}{x_2-\frac{1}{4}m^2}\\ = &\frac{y_1y_2-m(y_1+y_2)+m^2}{x_1x_2 - \frac{1}{4}m^2(x_1+x_2)+\frac{1}{16}m^4}\\ = &\frac{-4-4mt+m^2}{1-\frac{1}{4}m^2(4t^2+2)+\frac{1}{16}m^4}\\ = &\frac{-4-4mt+m^2}{1-m^2t^2-\frac{1}{2}m^2+\frac{1}{16}m^4} \end{aligned} $$
很难继续算下去。
另辟蹊径(双斜率)
上面的陷阱给了我们一个重要的启发: $$ \begin{aligned} &y_D\cdot y_E \\ = &m^2 + (1+\frac{1}{4}m^2)^2{\color{green}\frac{y_1-m}{x_1-\frac{1}{4}m^2}\cdot\frac{y_2-m}{x_2-\frac{1}{4}m^2}}\\ &-m(1+\frac{1}{4}m^2)({\color{green}\frac{y_1-m}{x_1-\frac{1}{4}m^2}+\frac{y_2-m}{x_2-\frac{1}{4}m^2}}) \end{aligned} $$
这里面绿色的不都是斜率嘛,我们直接设这些斜率不就完了。
也就是设: $$ AC:x=t_1(y-y_C)+x_C,\quad BC:x=t_2(y-y_C)+x_C $$
AC直接和抛物线联立得到: $$ y^2 - 4t_1y+4t_1y_C-4x_C=0 $$ 所以: $$ y_A+y_C = 4t_1 \implies y_A = 4t_1-y_C $$ 同理: $$ y_B = 4t_2-y_C $$
我们知道,$AB$过焦点等价于:
💡如果你不知道,这个结论实际上可以在几行就得到证明。
$$ y_Ay_B = -4 = (4t_1-y_C)(4t_2-y_C) $$
这是唯一的约束条件了,稍微整理就得到: $$ \color{blue}y_C(t_1+t_2) = 4t_1t_2+\frac{1}{4}y_C^2+1 = 4t_1t_2+x_C+1 $$
下面我们来计算$y_D\cdot y_E$,在AC、BC的方程里令$x=-1$立即得到: $$ \begin{aligned} &y_D\cdot y_E \\ = &(\frac{-1-x_C}{t_1}+y_C)(\frac{-1-x_C}{t_2}+y_C)\\ = &\frac{(1+x_C)^2}{t_1t_2}+y_C^2-(1+x_C)y_C(\frac{1}{t_1}+\frac{1}{t_2})\\ = & \frac{(1+x_C)^2 + t_1t_2y_C^2 - (1+x_C)y_C(t_1+t_2)}{t_1t_2} \end{aligned} $$
消去$y_C(t_1+t_2)$得到:
$$ \begin{aligned} &y_D\cdot y_E \\ = &\frac{(1+x_C)^2 + t_1t_2y_C^2 - (1+x_C)({\color{blue}4t_1t_2+x_C+1})}{t_1t_2}\\ = &\frac{t_1t_2y_C^2 - 4t_1t_2(1+x_C)}{t_1t_2}\\ = &\frac{4t_1t_2x_C - 4t_1t_2(1+x_C)}{t_1t_2} \\ = &-4 \end{aligned} $$
甚好!
反向结论
下面提到的数值仅在我们的题设中成立。
我们知道,在抛物线上两点的纵坐标乘积如果是$-4$,那么他们的连线肯定过焦点。
题干实际上告诉我们一个有趣的结论,在抛物线的准线上两点的纵坐标乘积如果是$-4$,那么他们对抛物线的同一点作割线,会产生焦点弦。