已知
四面体ABCD满足,角BAC=角ACD、角ABD=角BDC,证明:
$$ AB=CD $$ 一定成立,且 $$ AC=BD $$ 未必成立。
题解
AB等于CD
首先,我们设 $$ \alpha = \angle BAC = \angle ACD $$ 以及 $$ \beta = \angle ABD = \angle BCD $$
在高中知识里,为了利用空间里这些角的关系,我们只能借助向量了。
显然: $$ \vec{BD} = \vec{BA}+\vec{AC}+\vec{CD} $$
所以: $$ \begin{aligned} &|BD|\cdot|BA|\cos\beta\\ = &\vec{BD} \cdot \vec{BA}\\ = &|BA|^2 - |BA|\cdot|AC|\cos\alpha +\vec{CD}\cdot\vec{BA} \end{aligned} $$
同理 $$ \begin{aligned} &|BD|\cdot |CD|\cos \beta\\ =&\vec{BD} \cdot \vec{CD} \\ =&\vec{BA}\cdot\vec{CD} - |AC|\cdot|CD|\cos\alpha + |CD|^2 \end{aligned} $$
相减得到: $$ |BD|\cdot|BA|\cos\beta - |BD|\cdot |CD|\cos \beta \\ = |AC|\cdot|CD|\cos\alpha - |BA|\cdot|AC|\cos\alpha + |BA|^2-|CD|^2 $$
显然可以提出因子: $$ (|BA|-|CD|)(|BD|\cos\beta + |AC|\cos\alpha-|BA|-|CD|) = 0 $$ 此式在题设条件下恒成立。
显然 $$ |BD|\cos\beta + |AC|\cos\alpha - |BA|-|CD|=0 $$ 无法恒成立(例如对于正四面体它就不成立,对于任何$BD+AC=BA+CD$的四面体也不成立)。
所以 $$ |BA|-|CD| = 0 $$ 恒成立。
AC未必等于BD
我们现在已经知道了AB=CD恒成立,这时候我们可以很容易说明AC未必等于BD。
考虑BC=AD的特殊情况。
这时候根据余弦定理 $$ \angle BAC = \angle ACD $$ 一定成立。
所以我们在保持题设条件的情况下,可以通过旋转三角形BCD把AC的长度任意缩小:
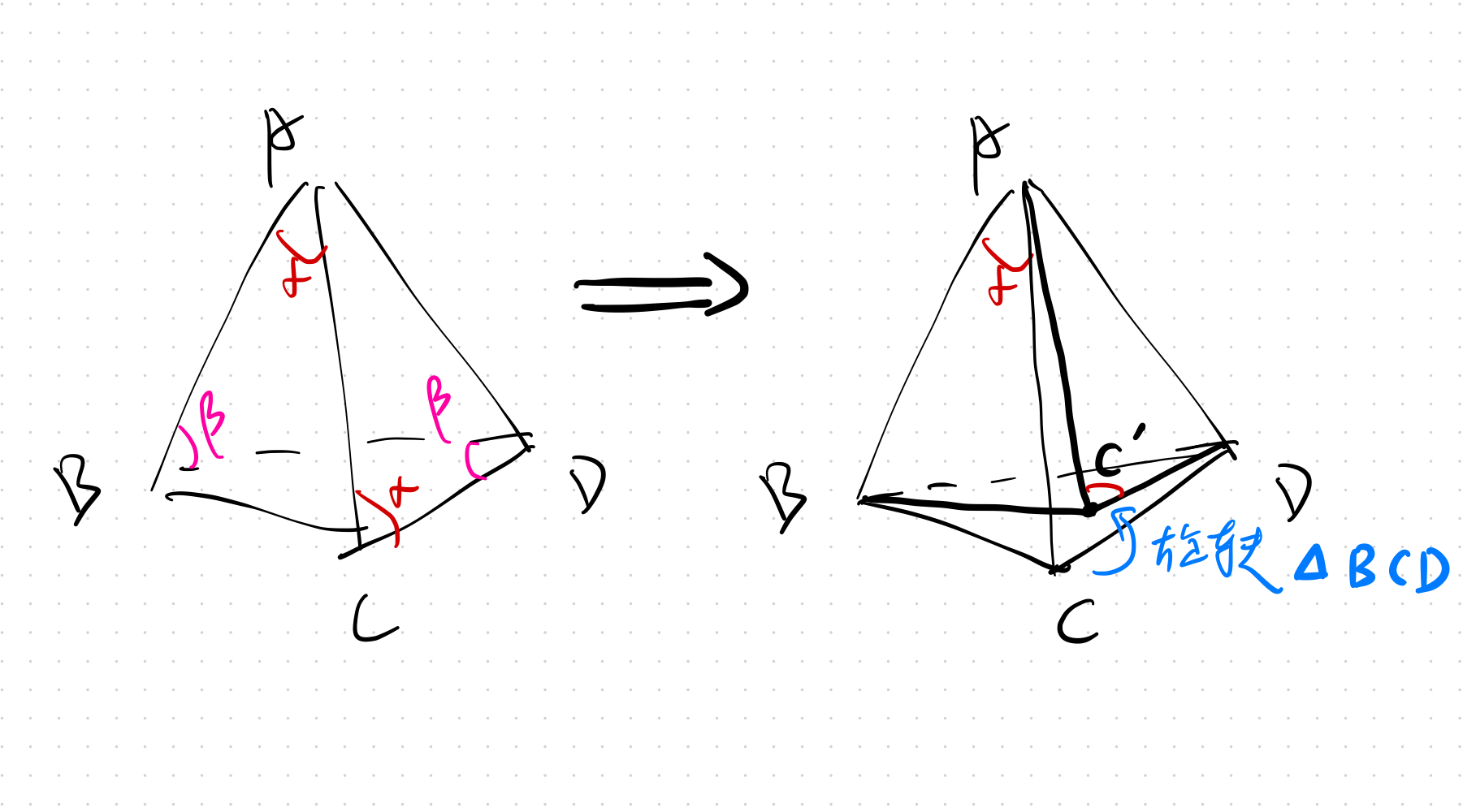
那么显然它不会恒等于BD。
几何体构造
某搜题软件上还有一种做法,但我觉得没什么价值,因为很难想到:

放在这里仅供参考。