已知
第一象限内,双曲线$x^2-y^2=2$上有一点$P(x_0,y_0)$,双曲线左右焦点分别为$F_1$和$F_2$证明:
$$ x_0 = \frac{|PF_1|+|PF_2|}{|PF_1|-|PF_2|} $$
此外,假设$PF_2$延长线交双曲线于$Q$点,且 $$ \vec{PF_2} = \lambda \vec{F_2}Q $$
$N$在$PF_1$上并且$PN=PF_2$,求 $$ S_{\triangle PQF_1} / S_{\triangle PNF_2} + \lambda $$ 的最小值。
题解
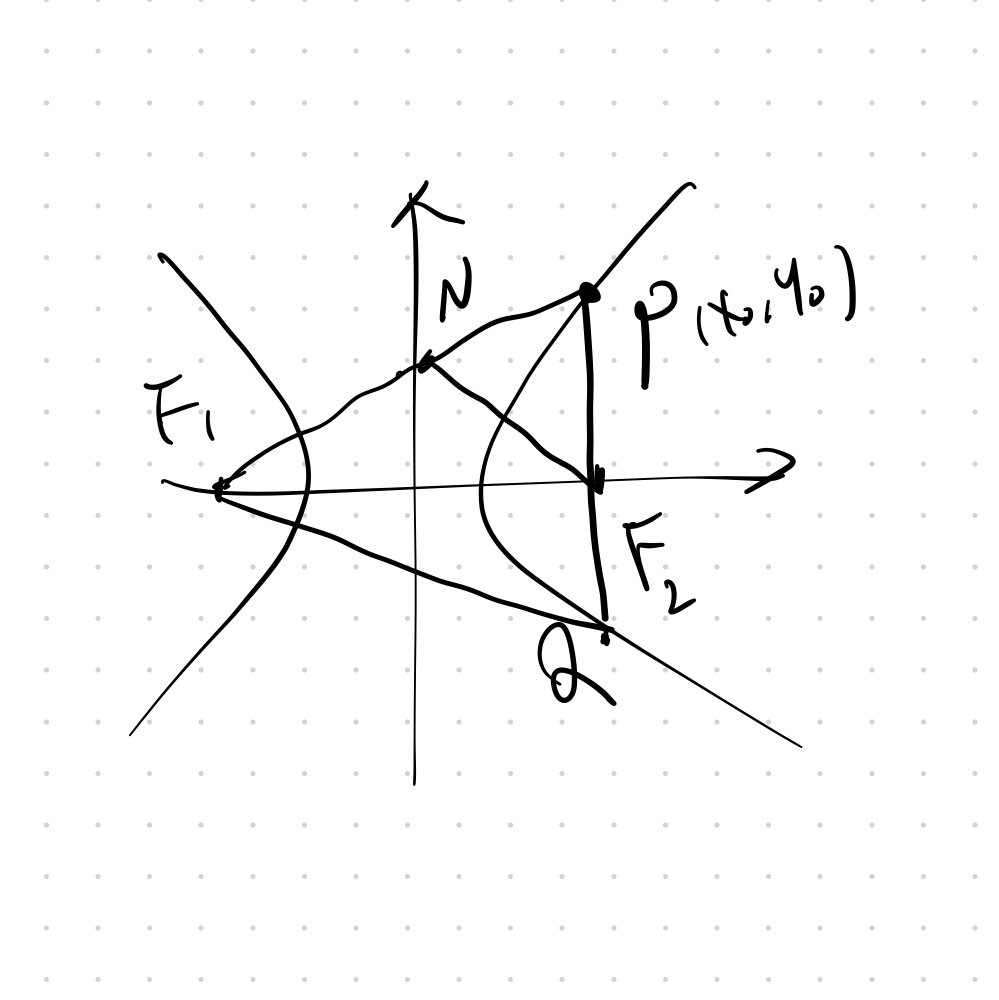
第一小问
这个题显然有非常多的做法。并且这个结论实际上和P点的位置无关,在其他象限也是成立的。
两点距离
显然,要求: $$ \frac{|PF_1|+|PF_2|}{|PF_1|-|PF_2|} $$ 只需要求: $$ \frac{PF_1}{PF_2} $$ 直接代入两点距离公式: $$ \frac{PF_1}{PF_2} = \frac{\sqrt{(x_0+2)^2+y_0^2}}{\sqrt{(x_0-2)^2+y_0^2}} $$ 我们知道: $$ y_0^2 = x_0^2-2 $$ 所以: $$ \frac{PF_1}{PF_2} = \frac{\sqrt{2x_0^2+4x_0+2}}{\sqrt{2x_0^2-4x_0+2}} = \frac{|x_0+1|}{|x_0-1|} $$ 反解出$x_0$即可。
准线
例如使用圆锥曲线统一定义,我们知道:
$$ PF_1 = e|x_0+\frac{a^2}{c}|, \quad PF_2 = e|x_0-\frac{a^2}{c}| $$
此题$c=2, a=\sqrt{2}, e=\sqrt{2}$,所以: $$ PF_1 = \sqrt{2}|x_0+1|, \quad PF_2 = \sqrt{2}|x_0-1| $$ 我们知道$x_0+1$和$x_0-1$一定符号相同。
所以: $$ PF_1+PF_2 = 2\sqrt{2}|x_0| $$
如果$x_0 \gt 0$,P点在第一象限就有: $$ PF_1 - PF_2 = 2a = 2\sqrt{2} $$ 反正则有: $$ PF_1 - PF_2 = -2\sqrt{2} $$ 综上我们知道:
$$ \frac{|PF_1|+|PF_2|}{|PF_1|-|PF_2|} = x_0 $$
向量
我们也可以用向量来做:
$$ \vec{PF_1} \cdot \vec{PF_2} = |PF_1|\cdot|PF_2|\cos<\vec{PF_1},\vec{PF_2}> $$
带入$P,F_1,F_2$的坐标,并且在$\triangle PF_1F_2$中使用余弦定理: $$ x_0^2-4+y_0^2 = \frac{PF_1^2+PF_2^2-16}{2} $$ 我们知道: $$ x_0^2-y_0^2=2 $$
所以: $$ PF_1^2+PF_2^2 = 4x_0^2+4 $$
根据双曲线第二定义。我们知道: $$ PF_1^2+PF_2^2 - 2PF_1\cdot PF_2 = 8 $$
所以: $$ PF_1\cdot PF_2 = 2x_0^2-2 $$ 所以: $$ PF_1+PF_2 = \sqrt{PF_1^2+PF_2^2 + 2PF_1\cdot PF_2} = \sqrt{8x_0^2} = 2\sqrt{2}|x_0| $$
至此就得到了和准线方法相同的结论。
第二小问
这里需要求三角形面积的比值,显然他们有共同角,所以使用面积公式得到: $$ S_{\triangle PQF_1} / S_{\triangle PNF_2} = \frac{PQ\cdot PF_1}{PN\cdot PF_2} $$ 其中 $$ PQ / PN = PQ / PF_2 = \frac{1+\lambda}{\lambda} $$ 所以我们只需要求 $$ \frac{PF_1}{PF_2} $$ 即可。
我们可以用韦达定理解决这问题,我就不写了,这里介绍另外一种纯粹的几何方法。
不妨假设$|QF_2|=t$,那么:
$$ PF_2 = \lambda t, PF_1 = 2\sqrt{2}+\lambda t, QF_1 = 2\sqrt{2}+ t $$
使用两次余弦定理(分别是$\triangle PF_1F_2$和$\triangle QF_1F_2$)可以得到:
$$ \frac{16+t^2-(2\sqrt{2}+ t)^2}{2\cdot t\cdot (2\sqrt{2}+ t)} = -\frac{16+\lambda^2t^2-(2\sqrt{2}+ \lambda t)^2}{2\cdot \lambda t\cdot (2\sqrt{2}+ \lambda t)} $$ 所以: $$ 16\lambda +\lambda t^2 - \lambda (2\sqrt{2}+ t)^2 + 16+\lambda^2t^2-(2\sqrt{2}+ \lambda t)^2 = 0 $$ 也就是: $$ 16\lambda +\lambda t^2 - 8\lambda - \lambda t^2 - 4\sqrt{2}\lambda t + 16+\lambda^2t^2-8-\lambda^2t^2-4\sqrt{2}\lambda t=0 $$
化简得到: $$ \lambda +1 -\sqrt{2}\lambda t =0 $$ 所以: $$ \lambda t = \frac{\lambda +1}{\sqrt{2}} $$ 所以: $$ PF_1 / PF_2 = 1+\frac{4}{\lambda +1} $$ 所以,最开始所求的面积比例为: $$ S_{\triangle PQF_1} / S_{\triangle PNF_2} = (1+\frac{4}{\lambda +1})(1+\frac{1}{\lambda}) = \frac{\lambda + 5}{\lambda} $$ 所以: $$ S_{\triangle PQF_1} / S_{\triangle PNF_2} + \lambda = 1+\lambda+\frac{5}{\lambda} \ge 1+2\sqrt{5} $$