已知

a∈Ra\in \mathbb{R}，对任意x>0x\gt 0都有 ((a−1)x−1)(x2−ax−1)≥0 \left((a-1)x-1\right)(x^2-ax-1)\ge 0 求a的值。

题解

特殊值

首先a≠1a\ne 1，带入检验一下就发现不成立了。

所以这是一个三次函数问题。

根的情况

其次，我们发现 x2−ax−1=0 x^2-ax-1=0 一定有不等实数根。再加上另外一个根 x=1a−1 x=\frac{1}{a-1}

所以三次函数要么有三个不等根，要么有二重实数根。

严格来说应该是零点，我就混着说了

无穷远

((a−1)x−1)(x2−ax−1)≥0 \left((a-1)x-1\right)(x^2-ax-1)\ge 0 再次，这个不等式要在x>0x\gt 0恒成立，所以a−1>0a-1\gt 0，否则正无穷一定不成立。

函数图像

综上所述，我们可以确定函数图像的一些性质： f(x)=((a−1)x−1)(x2−ax−1) f(x)=\left((a-1)x-1\right)(x^2-ax-1)

  • 至少两个零点
  • 有一个零点是1/(a−1)>01/(a-1) > 0
  • 图像走势是增减增

结合这三点，我们知道：函数肯定不能是三个不等的零点：

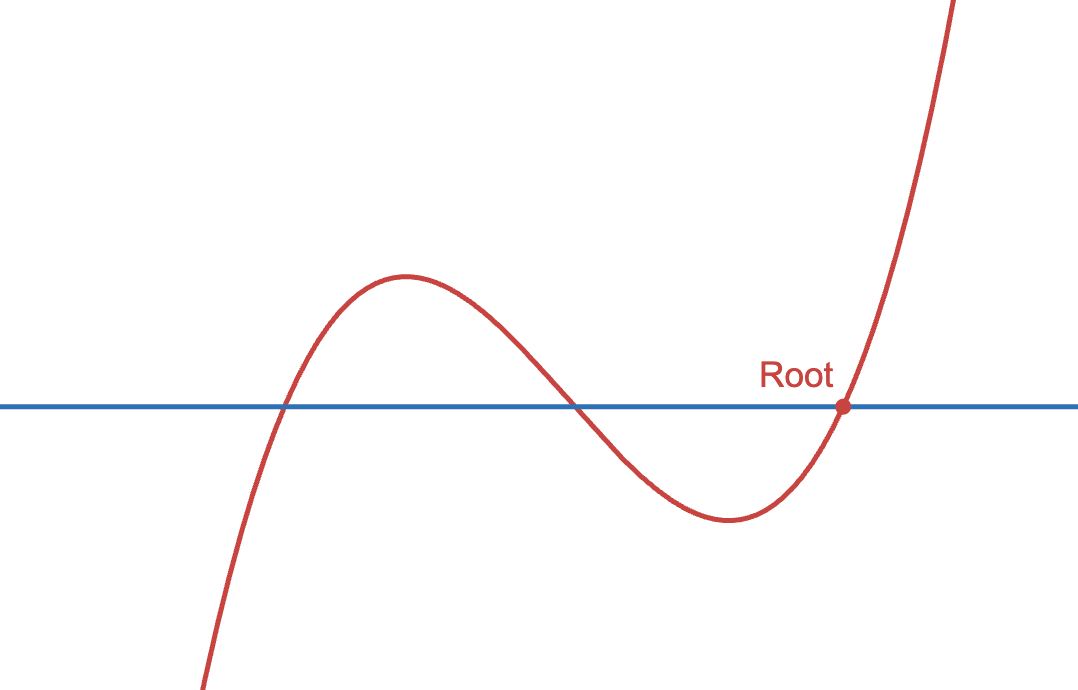
这种情况下，x>0x>0的范围内f(x)f(x)肯定有取值为负的部分。

所以f(x)f(x)存在重根。

也就是说：

1a−1 \frac{1}{a-1}

是 x2−ax−1=0 x^2-ax-1=0 的根。

带入得到： 1(a−1)2−aa−1−1=0 \frac{1}{(a-1)^2} - \frac{a}{a-1} - 1 = 0

也就是： 1−a(a−1)−(a−1)2=0 1- a(a-1)-(a-1)^2=0

整理一下： 2a2−3a=0 2a^2-3a=0 结合a−1>0a-1\gt 0的条件，得到： a=1.5 a = 1.5

这时候图像恰和x轴相切：