已知
$$ x+y+z = 5 $$ 和 $$ xy+yz+xz = 3 $$
求$z$的范围
题解
二次方程韦达定理
把$z$视为参数: $$ x+y = 5-z\\ xy = 3-z(x+y) = 3-z(5-z) $$ 于是$x,y$是下述方程的两个根: $$ t^2-(5-z)t+3-z(5-z)=0 $$ 只要$z$的取值范围使得此方程有解即可找到满足题设的$x,y$,令 $$ \Delta = (5-z)^2-4(3-z(5-z))\ge 0 $$ 即可解得: $$ z \in [-1,\frac{13}{3}] $$
三次方程韦达定理
设 $$ xyz = \theta $$ 那么$x,y,z$是方程 $$ f(t) = t^3-5t^2+3t=\theta $$ 的三个根:
如图所示,绿色是$f(t)$的图像,黑色是$z$取最大值时$\theta$的位置,紫色时最小值时$\theta$的位置。
令: $$ f’(t) = 3t^2-10t+3=0 $$ 得到极值点: $$ t_1 = 3,\quad t_2=\frac{1}{3} $$
设方程 $$ f(t) = f(t_1) $$
得到: $$ t^3-5t^2+3t = t_1^3-5t_1^2+3t_1 $$
根据图像,我们知道$t=t_1$一定是该方程的二重根,考虑$t\ne t_1$的第三个根$t_{m}$(实际上这就是所求的$z$的最小值),使用韦达定理得到: $$ t_1+t_1 + t_m = 5 $$
实际上我们可以做因式分解: $$ \begin{aligned} &t^3-5t^2+3t = t_1^3-5t_1^2+3t_1\\ \iff &t^3-t_1^3 -5(t^2-t_1^2)+3(t-t_1)=0\\ \iff &(t-t_1)(t^2+t_1^2+tt_1-5(t+t_1)+3)=0\\ \iff &(t-t_1)^2(t-5+2t_1)=0 \end{aligned} $$
于是 $$ z_{\mathrm{min}} = t_m = 5-2t_1 = -1 $$
同理 $$ z_{\mathrm{max}} = t_M = 5-2t_2 = \frac{13}{3} $$
立体几何
显然: $$ x^2+y^2+z^2 = (x+y+z)^2-2(xy+yz+xz) = 19 $$
于是$(x,y,z)$是三维空间内球面上的一点。
结合另外一个平面约束: $$ x+y+z = 5 $$ 我们可以知道$(x,y,z)$在如图所示的圆上运动:
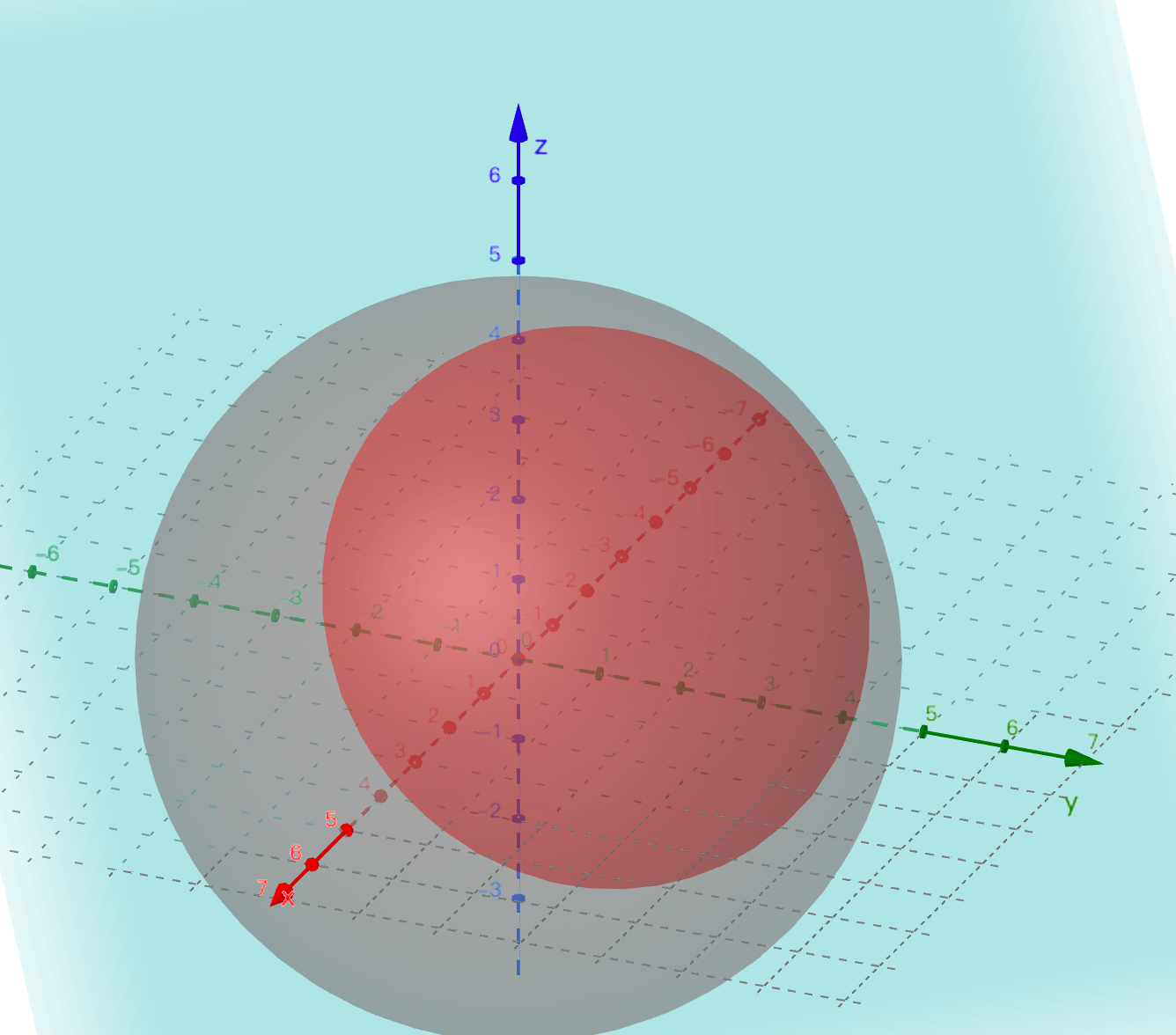
根据对称性,$z$的最大最小值都$x=y$的时候取到: $$ x = y\\ x+y+z = 5\\ xy+yz+xz = 3 $$
于是 $$ z = 5-2x = \frac{3-x^2}{2x} $$
也就是 $$ 3x^2-10x+3=0 \\ \implies x_1=3,\quad x_2=\frac{1}{3} $$
所以$z$的范围是: $$ z \in [-1,\frac{13}{3}] $$
平面几何
$$ x^2+y^2+z^2 = 19\\ x+y+z=5 $$ 消去$z$得到 $$ x^2+y^2+(5-x-y)^2=19 $$ 这是一个椭圆:
我们要的是 $$ z = 5-(x+y) $$
显然$x=y$的时候取到最大、最小值。
实际上,平面几何就是立体几何在$z=0$平面上的投影。